測定した調査や記録の分析に、「代表値」と呼ばれる平均値、中央値、最頻値が役立ちます。代表値を使うことで、データの特徴を示すことができます。
ただし、代表値はいつどんな場面でも万能というわけではありません。例えば平均値を求めたい時に、極端に大きな数値が混じっていた場合、結果が引っ張られてしまうこともあるからです。また、データ全体の傾向を知りたい場合には、代表値のみでは捉えることができないため、散布度など別指標を参考にする必要があります。
本記事では、3つの代表値「平均値」「中央値」「最頻値」の特徴と使い分け方法、扱う際の注意点について解説します。
平均値、中央値、最頻値とは
基本統計量には、「代表値」と「散布度」があります。「代表値」はデータの中心的な傾向を表す値、「散布度」はデータ全体の散らばり具合を表す値です。平均値、中央値、最頻値は、これらのうち「代表値」に相当する値です。
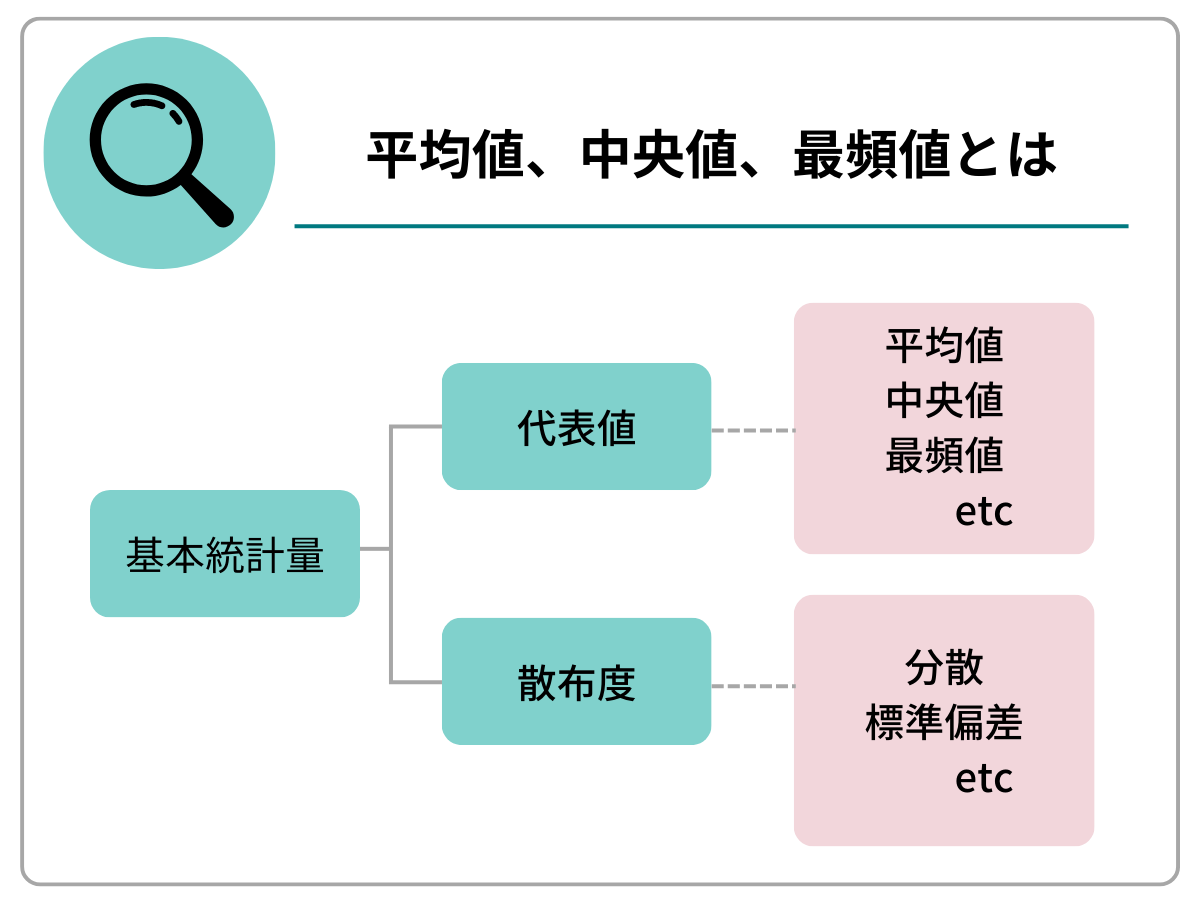
平均値
平均値は、データの総和をデータの個数で割った値です。例えば、調査対象者5名のスマホ利用時間が以下の通りだったとします。
| 調査対象者 | A | B | C | D | E |
|---|---|---|---|---|---|
| スマホ利用時間(H/日) | 2.5 | 3 | 0.5 | 1 | 6 |
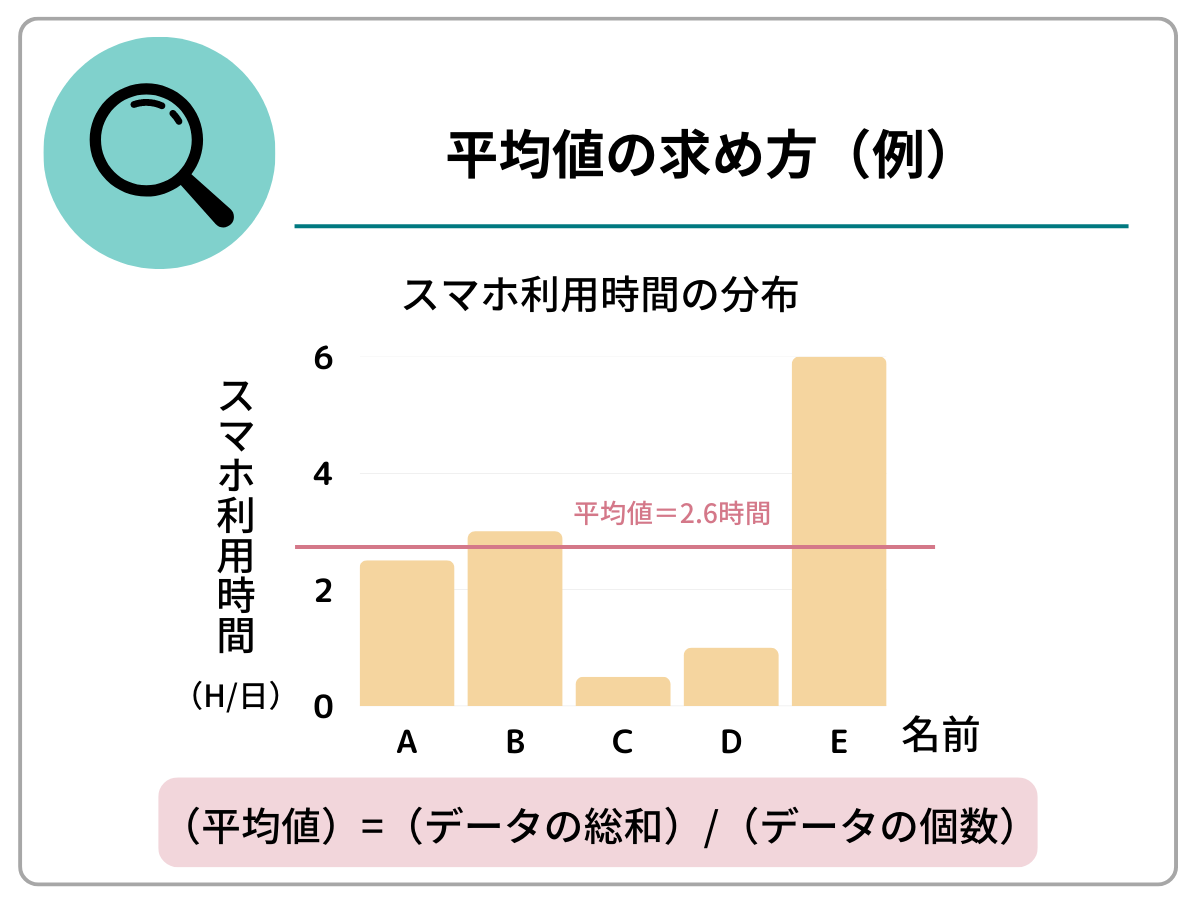
このとき、スマホ利用時間の平均値は以下のように求められます。
(平均値)=(2.5+3+0.5+1+6)/5=2.6(時間)
中央値
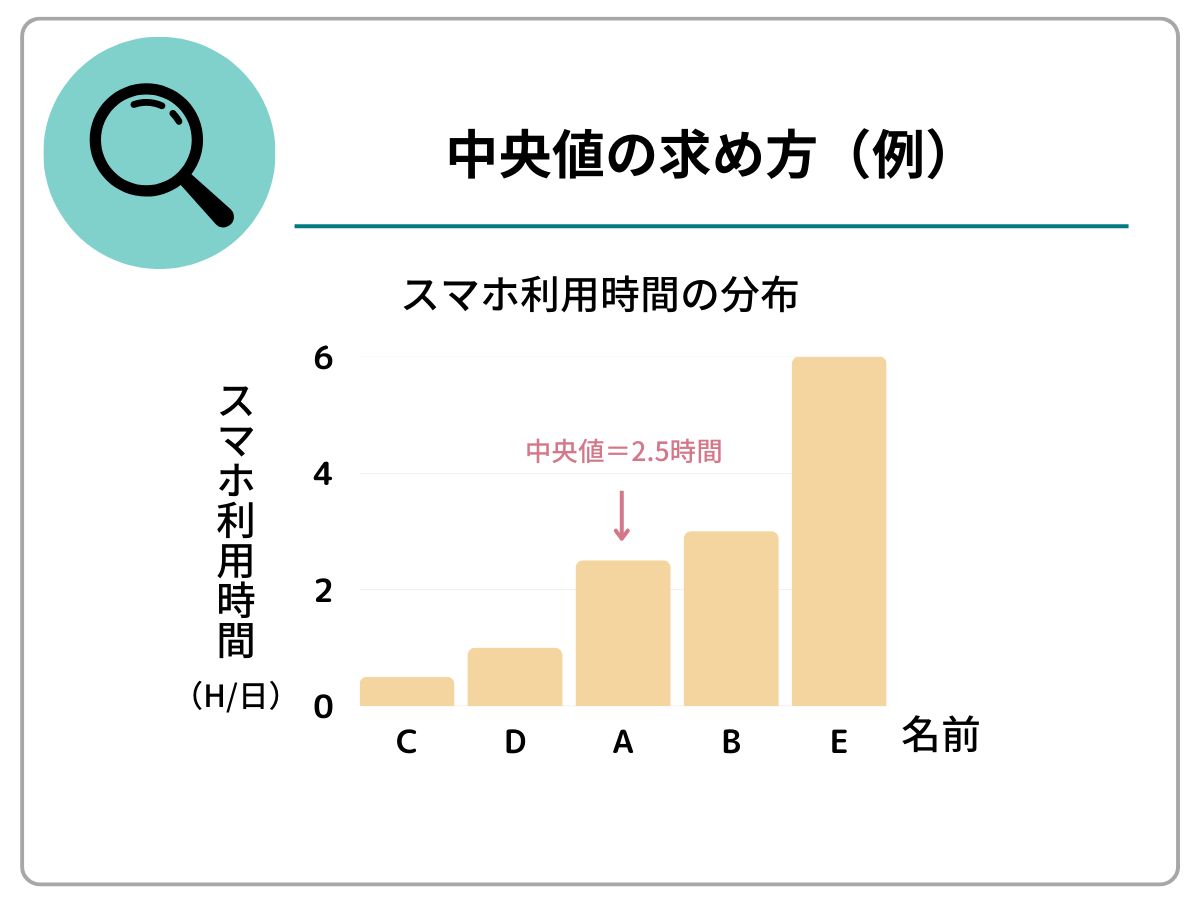
中央値は、すべてのデータを小さい順に並べたとき、中央に位置する値です。先ほどの例と同じデータで、中央値を求めてみましょう。
まず、データを数値の小さい順に並べ替えます。
| 名前 | C | D | A | B | E |
|---|---|---|---|---|---|
| スマホ利用時間(H) | 0.5 | 1 | 2.5 | 3 | 6 |
データの個数が奇数のとき、データのちょうど真ん中が中央値です。偶数の場合は、真ん中に相当する値2つの平均が中央値です。
今回はデータの個数が5つ(奇数)なので、3番目に位置する2.5時間が中央値に相当します。
最頻値
最頻値は、データの中で最も登場回数の多いデータの個数を指します。例えば、ある商品Xの購入数が以下だったとします。
| 名前 | A | B | C | D | E |
|---|---|---|---|---|---|
| 商品Xの購入数(個) | 2 | 1 | 2 | 2 | 4 |

このとき、A、C、Dの3人が2個、Bが1個、Eが4個購入しています。よって最頻値は2個です。
平均値、中央値、最頻値はどう使い分けるべき?
それぞれの代表値ごとに、求め方や示す値は異なります。そのためデータの傾向や、つかみたい特徴によって最適な代表値も変わってきます。
本章では、代表値ごとのデータの特性と、使い分けの視点について解説します。
平均値の扱い方
平均値は、全データの中心を知りたい時に有効ですが、扱うデータの中に外れ値がある場合、思うような結果を得ることができません。
先ほどのスマートフォン利用時間を例に、平均値を見てみましょう。もし、1日15時間と極端な利用をしている人がいると、利用時間の平均は約4.7時間となってしまいます。
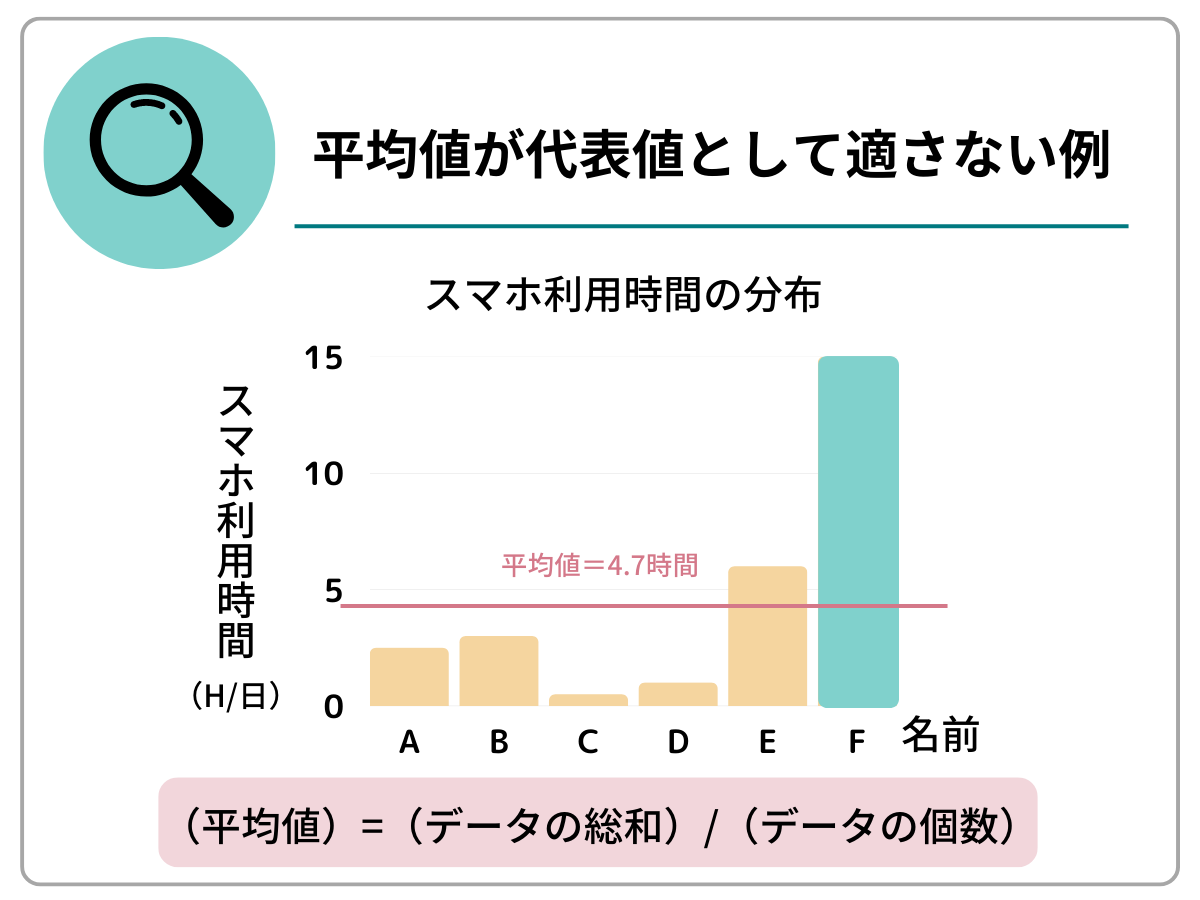
極端な値に引っ張られてしまうと、データの特徴を表しているとはいえないため、データに外れ値がある場合、平均値は不適となります。もしデータの中に外れ値がある場合は、中央値を用いるとよいでしょう。
中央値の扱い方
中央値は、外れ値が含まれたりばらつきが大きかったりする際、中央の値を知りたい場合に有効です。
中央値の算出には、「小さい順に並び替える」→「中央にある数値を見つける」という手順を踏みます。もしデータに外れ値があった場合でも、読み取るのは中央にあるデータに限ります。そのため、外れ値の影響を受けづらいのです。
しかし中央値は、中央にある値以外のデータを十分に活用することができません。また、データのばらつきが大きくても小さくても、中央値は同じになることがあります。
最頻値の扱い方
最頻値も中央値と同様、外れ値があってもピークなどの傾向を把握できます。同じ値の外れ値が出ることは滅多にないため、分析の邪魔をしないのです。
ただ、最頻値が複数になる場合があることには留意しておく必要があります。平均値や中央値は1つの値しかとりませんが、最頻値は2つ以上になる可能性があります。この場合、データの傾向を示す代表値としての意味が薄れてしまいます。
また、データ数が少なかったり、データ間の差がない場合に使えないのも最頻値の特徴です。例えば、商品Xの購入数ごとの人数の最頻値を知りたいとします。
| 商品Xの購入数(個) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 人数(人) | 1 | 1 | 1 | 1 | 1 |
全てのデータが同じもしくは異なる値を取ってしまうと、最頻値ではデータ全体の特徴をつかむことができません。外れ値があっても対応できる一方で、データによっては効果を発揮できない点には留意しましょう。
代表値を扱う際の注意点
ここまで、3つの代表値の計算方法や使い分けについて解説してきました。最後に、データ分析で実際に代表値を扱うときに気をつけるポイントについて解説します。
全体の分布によって扱う値を決める
それぞれの代表値ごとに、算出できる値は異なります。まずは全体の分布をチェックしたうえで扱う値を決めましょう。
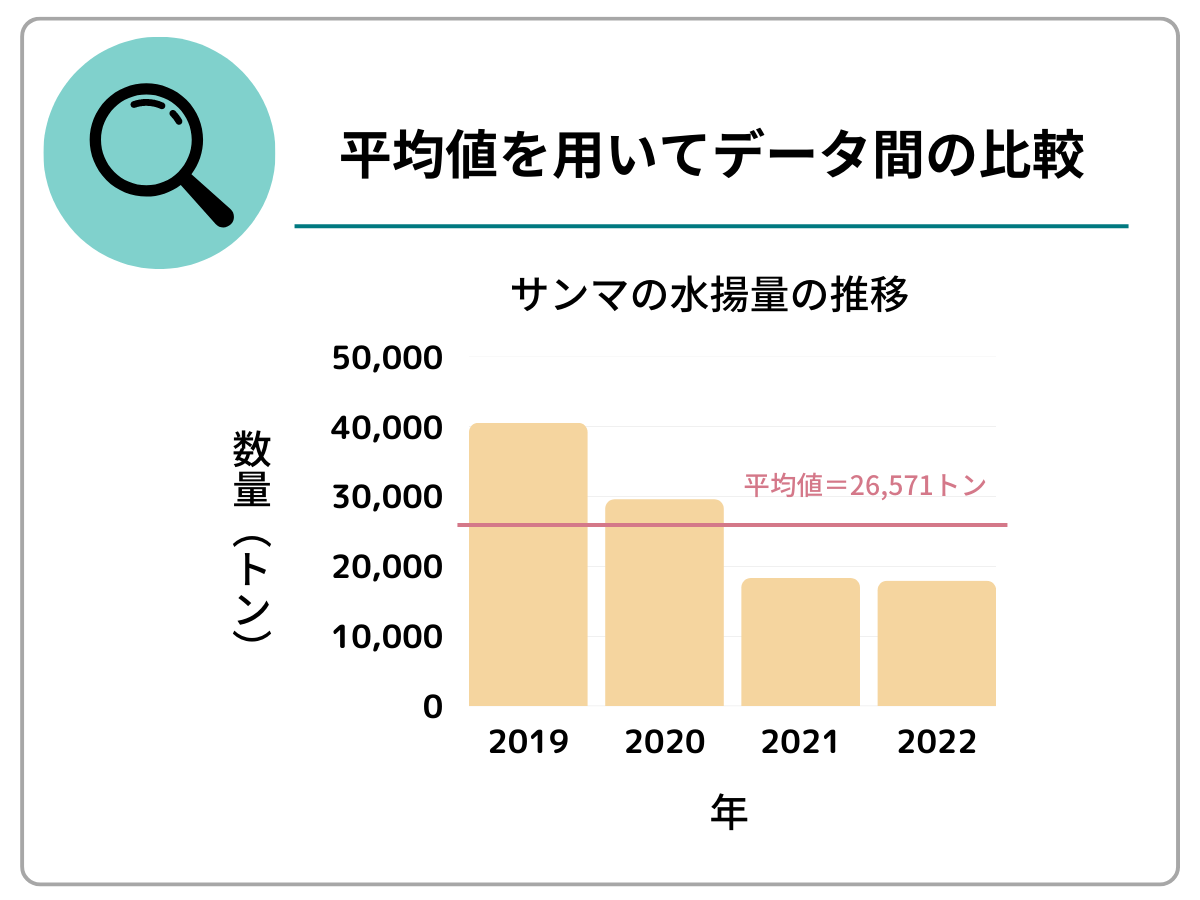
例えば「漁獲量の年度ごとの比較」のようにデータ全体の変化を比較したい場合や、「A社とB社の年収の比較」のようにデータ間の比較を行いたい場合には平均値を活用し、外れ値が含まれている場合は中央値、最頻値を検討するとよいでしょう。
複数の観点からデータを見るようにする
代表値1つだけでデータの特性を正確に表すことはできません。
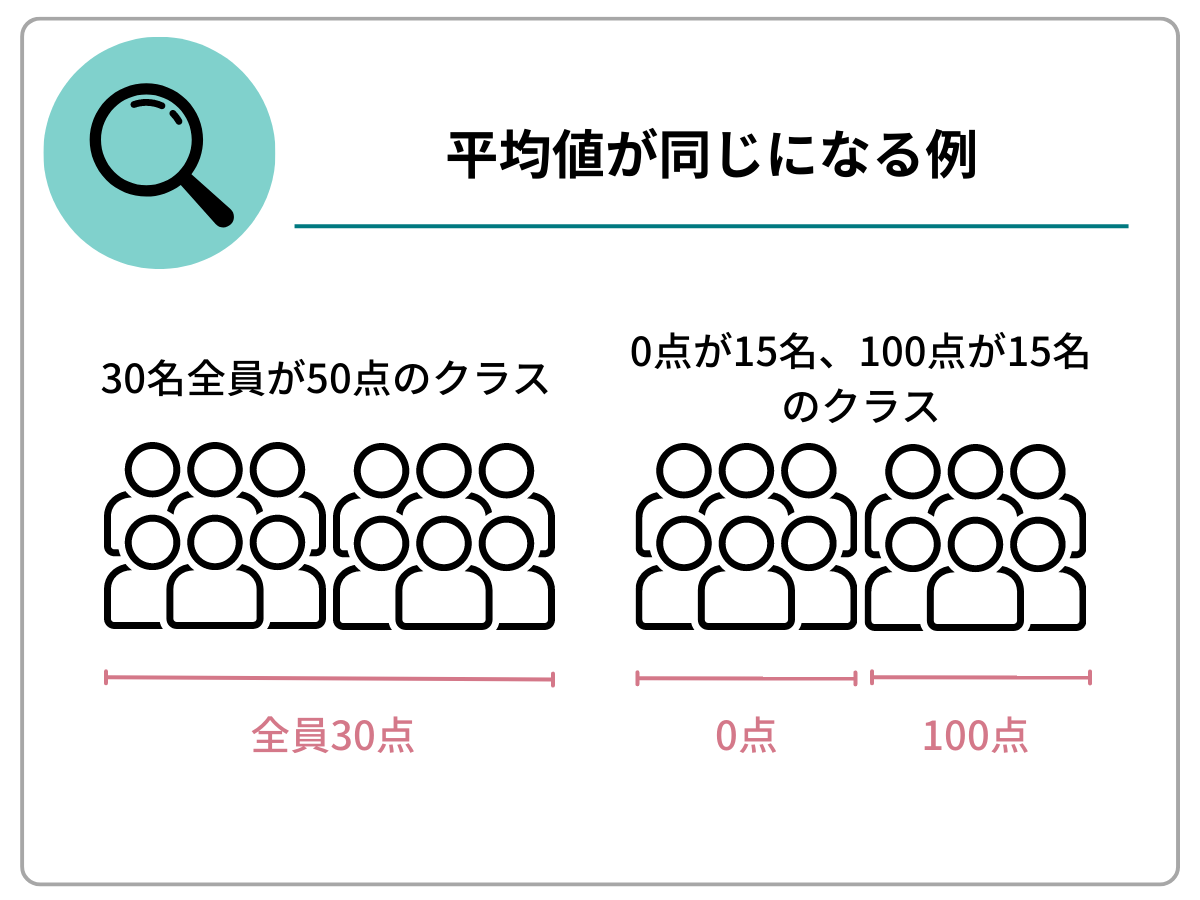
例えば、30名から成る2つのクラスの試験の平均点がどちらも50点だったとします。30名全員が50点だったクラスと、15名が0点で残りの15名が100点のクラスでは生徒の学力が同じとは言えません。複数の指標からデータを見ることが重要です。
代表値ではデータ全体の様子を捉えられない
代表値はデータ全体の特徴をつかむものですが、散らばり具合を反映することができないため、データの全体の様子を捉えるには不十分です。「散らばり」とは、「平均からどれだけ離れているか」を示す指標です。
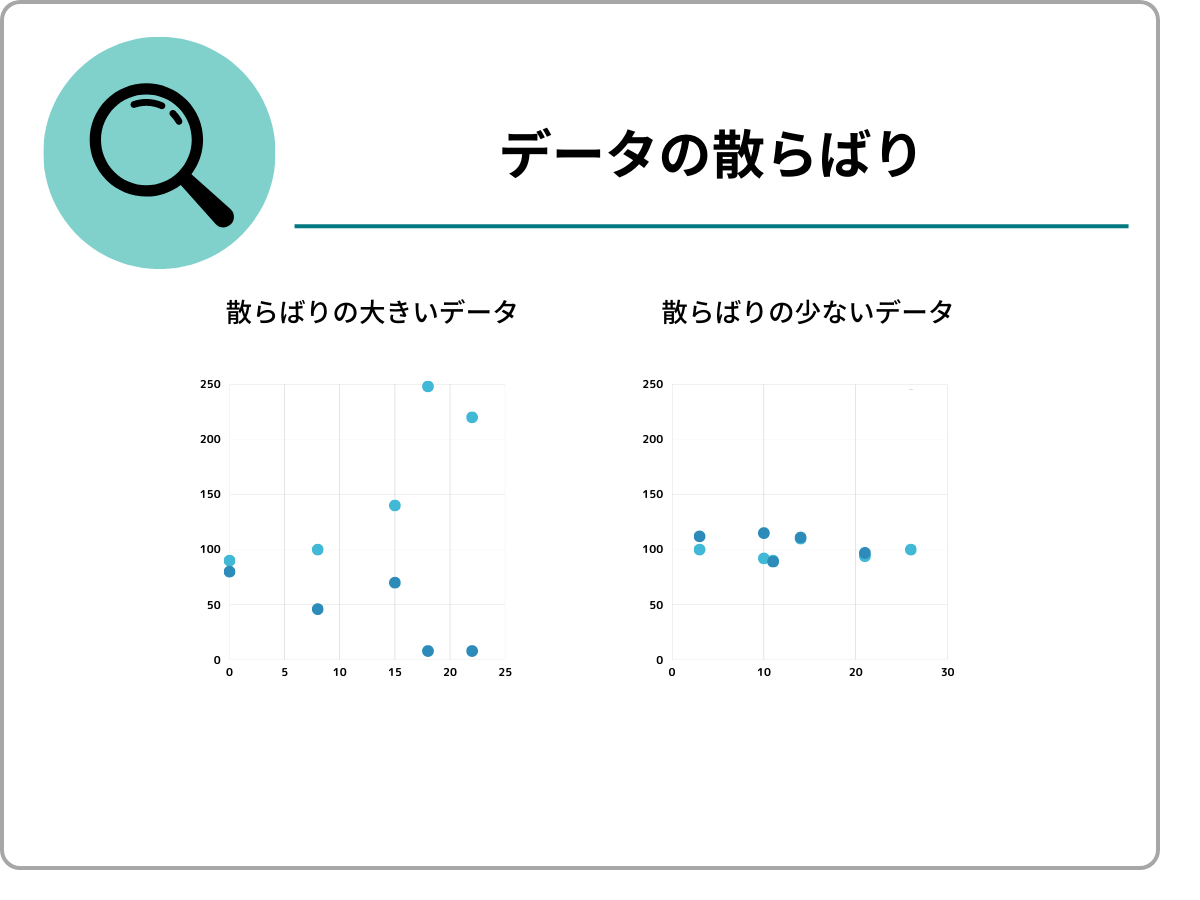
データの散らばり具合を示す指標として、散布度があり、「分散」「標準偏差」がこれに該当します。
標準偏差について詳しく知りたい方は、「標準偏差とは?ビジネスでの活用方法と求め方を解説」の記事をご覧ください。
まとめ
代表値には「平均値」「中央値」「最頻値」の3種類があり、データ全体の中心的な傾向を知りたい時に用いられます。どれもエクセルやスプレッドシートの関数で簡単に出力できるため、自身で簡単に確認しやすいのが特徴です。
とはいえ、外れ値の有無やデータ量などによって、最適な代表値は異なります。また、データの散らばりを知りたい際には、代表値ではなく散布度を確認することで、全体の様子をつかむことができます。
1つの統計量にこだわらず、何を知りたいのか、状況に応じて使い分けるようにしましょう。
完全DIY型アンケートプラットフォームのGMO Ask

GMO Askは、完全DIY型のアンケートプラットフォームです。調査の企画や設計に時間をかけず、短期間で調査を行うことが可能です。また、調査データはエクセルやスプレッドシートで出力できるため、ご自身で簡単に確認できます。
【サービスの特徴】
- アンケート作成から配信まで、すべて自身で行うことができる
- 約3,000万人ものアンケートモニター
- 1問1回答10円。分かりやすい料金体系
あなたの会社でも、GMO Askを使って、スピーディに調査を実施してみませんか。